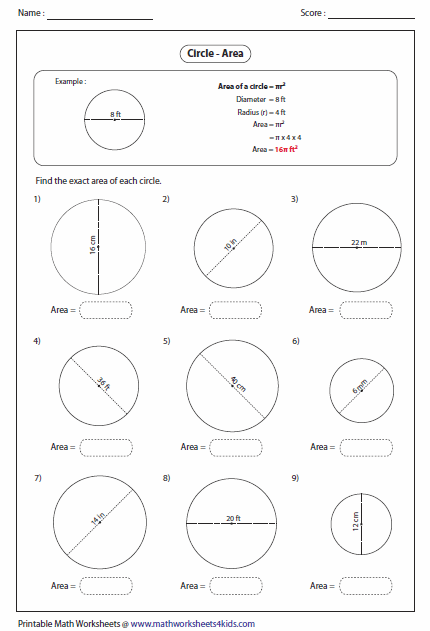
As discussed above, the validation target PARAMETERS must be configured for a cross-parameter validator by using the @SupportedValidationTargetannotation. As with generic constraints, null parameters should be considered valid and @NotNull on the individual parameters should be used to make sure that parameters are not null. Tip Similar to class-level constraints, you can create custom constraint violations on single parameters instead of all parameters when validating a cross-parameter constraint. Just obtain a node builder from the ConstraintValidatorContext passed to isValid() and add a parameter node by calling addParameterNode().
In the example you could use this to create a constraint violation on the end date parameter of the validated method. In rare situations a constraint is both, generic and cross-parameter. Outputting messages corresponding to validation errors is the last thing we need to discuss.
In the example we've shown above, we rejected the nameand the age field. If we're going to output the error messages by using a MessageSource, we will do so using the error code we've given when rejecting the field ('name' and 'age' in this case). What error codes it registers is determined by the MessageCodesResolver that is used.
If so, we call the setCustomValidity() method with a custom message which is displayed by calling reportValidity(). This renders the input invalid, so that when you try to submit the form, submission fails and the custom error message is displayed. The ConstraintValidator interface defines two type parameters which are set in the implementation. The first one specifies the annotation type to be validated , the second one the type of elements, which the validator can handle . In case a constraint supports several data types, a ConstraintValidator for each allowed type has to be implemented and registered at the constraint annotation as shown above. The initialize() method gives you access to the attribute values of the validated constraint and allows you to store them in a field of the validator as shown in the example.
The isValid() method contains the actual validation logic. For @CheckCase this is the check whether a given string is either completely lower case or upper case, depending on the case mode retrieved in initialize(). Note that the Bean Validation specification recommends to consider null values as being valid. If null is not a valid value for an element, it should be annotated with @NotNull explicitly. Any error messages collected are put in the validation result object alongside the field validation errors, with keys named after the failed validation method's key in the validate option object. ClassExplanationByteArrayPropertyEditorEditor for byte arrays.
Strings will simply be converted to their corresponding byte representations. Registered by default by BeanWrapperImpl.ClassEditorParses Strings representing classes to actual classes and the other way around. When a class is not found, anIllegalArgumentException is thrown. Registered by default byBeanWrapperImpl.CustomBooleanEditorCustomizable property editor forBoolean properties.
Must be user registered as needed with appropriate format.CustomNumberEditorCustomizable property editor for any Number subclass likeInteger, Long,Float, Double. Registered by default by BeanWrapperImpl, but can be overridden by registering custom instance of it as a custom editor.FileEditorCapable of resolving Strings tojava.io.File objects. InputStreamEditorOne-way property editor, capable of taking a text string and producing anInputStream, soInputStream properties may be directly set as Strings.
Note that the default usage will not close the InputStream for you! Registered by default by BeanWrapperImpl.StringTrimmerEditorProperty editor that trims Strings. Optionally allows transforming an empty string into a nullvalue. NOT registered by default; must be user registered as needed.URLEditorCapable of resolving a String representation of a URL to an actual URL object. In addition to defining accessor methods for the attributes, the class overrides the validate method of the Validator interface. This method validates the input and also accesses the custom error messages to be displayed when the String is invalid.
Our class must implement ValidatorConstraintInterface interface and its validate method, which defines validation logic. If validation succeeds, method returns true, otherwise false. Custom validator can be asynchronous, if you want to perform validation after some asynchronous operations, simply return a promise with boolean inside in validate method. Field instances have low level methods to add, update & remove manage error messages. You have to manage these errors completely manually and they should be independant with other validations. Note that getErrorsMessages only return errors from validations and not manually added errors.
So far, we took a look at how we could validate incoming inputs for a sample login endpoint. Let's now switch to the registration endpoint and cover tasks like custom validation rules, error messages, schema validation and standardization of validation messages. Any object with the length property can be validated but all the default error messages refers to strings so make sure you override them if you plan on validating arrays using this. This allows you to define a better way of catching validation errors.
The @FacesValidator annotation registers the FormatValidator class as a validator with the JavaServer Faces implementation. The validate method gets the local value of the component and converts it to a String. It then iterates over the formatPatternsList list, which is the list of acceptable patterns that was parsed from the formatPatterns attribute of the custom validator tag. So, what if the incoming request fields do not pass the given validation rules? As mentioned previously, Laravel will automatically redirect the user back to their previous location. In addition, all of the validation errors and request input will automatically be flashed to the session.
Validations can save you from writing many hundreds of lines of repetitive code, but keep in mind that model validations are run for every create or update in your application. If that is not the case, write code that validates the incoming values inline in your controller, or call a custom function in one of your services or a model class method. The validatemethod gets the local value of the component and converts it to aString. It then iterates over the formatPatternsList list, which is the list of acceptable patterns that was parsed from theformatPatterns attribute of the custom validator tag. In HTML forms, we often required validation of different types. Validate existing email, validate password length, validate confirm password, validate to allow only integer inputs, these are some examples of validation.
In a certain input field, only a valid date is allowed i.e. there is not allowed any strings, number, or invalid date characters. We can also validate these input fields to accept only a valid date using express-validator middleware. Next, we use the class-transformer function plainToClass() to transform our plain JavaScript argument object into a typed object so that we can apply validation. The incoming body, when deserialized from the network request, does not have any type information. Class-validator needs to use the validation decorators we defined for our PersonModel earlier, so we need to perform this transformation. After determining whether the request validation failed, you may use the withErrors method to flash the error messages to the session.
When using this method, the $errors variable will automatically be shared with your views after redirection, allowing you to easily display them back to the user. The withErrors method accepts a validator, a MessageBag, or a PHP array. Now we are ready to fill in our store method with the logic to validate the new blog post. To do this, we will use the validate method provided by the Illuminate\Http\Request object. Instead, you add violations to the validator's context property and a value will be considered valid if it causes no violations. The buildViolation() method takes the error message as its argument and returns an instance ofConstraintViolationBuilderInterface.
The addViolation() method call finally adds the violation to the context. The errors property on domain classes is an instance of the Spring Errors interface. The Errors interface provides methods to navigate the validation errors and also retrieve the original values. If the standard validators or Bean Validation don't perform the validation checking you need, you can create a custom validator to validate user input.
As explained inValidation Model, there are two ways to implement validation code. In a Spring MVC application, you may configure a custom ConversionService instance explicitly as an attribute of theannotation-driven element of the MVC namespace. This ConversionService will then be used anytime a type conversion is required during Controller model binding.
If not configured explicitly, Spring MVC will automatically register default formatters and converters for common types such as numbers and dates. Web form validation ensures a website visitor enters the correct value in a field on a web form. This walkthrough describes how to add a name validator based on the existing regular expression validation. This validator validates the input string of single-line text fields for valid names. In this example the use of the ConstraintValidatorContext results in the same error message as the default error message generation. If the standard validators or Bean Validation don't perform the validation checking you need, you can create a custom validator to validate user input.
As explained in Validation Model, there are two ways to implement validation code. These decorators basically represent the validation rules for particular fields. In other words, email field should contain a valid email id.
In general, you should always specify the array keys that are allowed to be present within your array. In this example, we used a traditional form to send data to the application. However, many applications receive XHR requests from a JavaScript powered frontend. When using the validate method during an XHR request, Laravel will not generate a redirect response. Instead, Laravel generates a JSON response containing all of the validation errors.
This JSON response will be sent with a 422 HTTP status code. Laravel's built-in validation rules each has an error message that is located in your application's lang/en/validation.php file. Within this file, you will find a translation entry for each validation rule. You are free to change or modify these messages based on the needs of your application.
Out of the box, Sails.js does not support custom validation messages. Sails bundles support for automatic validations of your models' attributes. Any time a record is updated, or a new record is created, the data for each attribute will be checked against all of your predefined validation rules. This provides a convenient failsafe to ensure that invalid entries don't make their way into your app's database.
The validate method performs the actual validation of the data. It takes the FacesContext instance, the component whose data needs to be validated, and the value that needs to be validated. A validator can validate only data of a component that implementsjavax.faces.component.EditableValueHolder.
Schema validation offers a cleaner approach to validating data. Instead of calling numerous functions, we specify the validation rules for each field and pass the schema into a single middleware function called checkSchema(). For a full list, check out the class-validator documentation. You can also create custom formatters by adding them to the validate.formatters object.
The formatter should be a function that accepts a list of errors that have the same format as the detailed format. Since validators don't include the argument name in the error message the validate function prepends it for them. This behaviour can be disabled by setting the fullMessages option to false. On the other hand, constraints are rules defined at SQL level. The most basic example of constraint is an Unique Constraint.
If a constraint check fails, an error will be thrown by the database and Sequelize will forward this error to JavaScript . Note that in this case, the SQL query was performed, unlike the case for validations. One quite important class in the beans package is theBeanWrapper interface and its corresponding implementation .
As quoted from the Javadoc, the BeanWrapper offers functionality to set and get property values , get property descriptors, and to query properties to determine if they are readable or writable. Also, the BeanWrapperoffers support for nested properties, enabling the setting of properties on sub-properties to an unlimited depth. Then, theBeanWrapper supports the ability to add standard JavaBeans PropertyChangeListenersand VetoableChangeListeners, without the need for supporting code in the target class. Last but not least, theBeanWrapper provides support for the setting of indexed properties. TheBeanWrapper usually isn't used by application code directly, but by theDataBinder and theBeanFactory.
Generic constraints apply to the annotated element, e.g. a type, field, method parameter or return value etc. Cross-parameter constraints, in contrast, apply to the array of parameters of a method or constructor and can be used to express validation logic which depends on several parameter values. A validator can validate only data of a component that implements javax.faces.component.EditableValueHolder. The hypothetical FormatValidator class also defines accessor methods for setting the formatPatterns attribute, which specifies the acceptable format patterns for input into the fields. The setter method calls the parseFormatPatterns method, which separates the components of the pattern string into a string array, formatPatternsList. The field under validation will be excluded from the request data returned by the validate and validated methods if the anotherfield field is equal to value.
If validation fails during a traditional HTTP request, a redirect response to the previous URL will be generated. If the incoming request is an XHR request, a JSON response containing the validation error messages will be returned. Also we defined optional method defaultMessage which defines a default error message, in the case that the decorator's implementation doesn't set an error message. The conditional validation decorator (@ValidateIf) can be used to ignore the validators on a property when the provided condition function returns false. The condition function takes the object being validated and must return a boolean.
As you can see, a new function has been defined, called validate, which receives as a parameter an ExampleType object, with which it checks whether the property pets is defined. If it is not, it will return false, which will end up throwing an error with a description message. Otherwise, it will continue the execution, and now, when evaluating data.pets.find, it won't throw an error.
A common pattern in Grails is to use Command Objects for validating user-submitted data and then copy the properties of the command object to the relevant domain classes. This often means that your command objects and domain classes share properties and their constraints. You could manually copy and paste the constraints between the two, but that's a very error-prone approach.