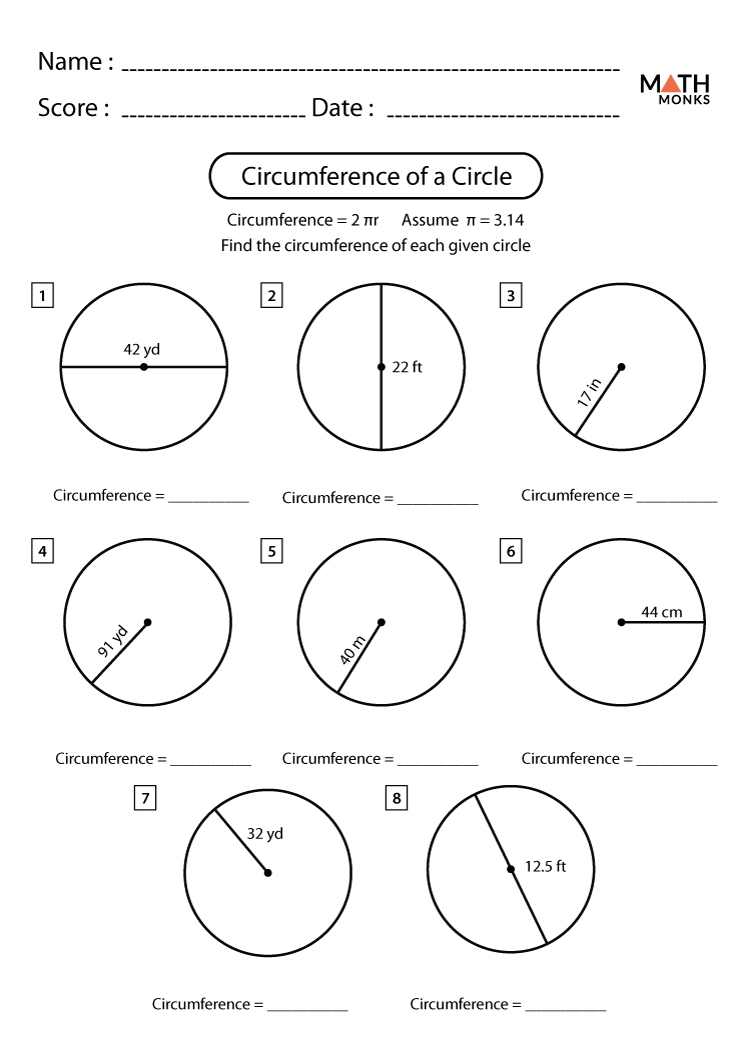
The circle is a two-dimensional shape, which possesses its area and perimeter. The perimeter of the circle is also termed as the circumference, which is the measure around the circle. The area of the circle is the region defined by it in a 2D plane.
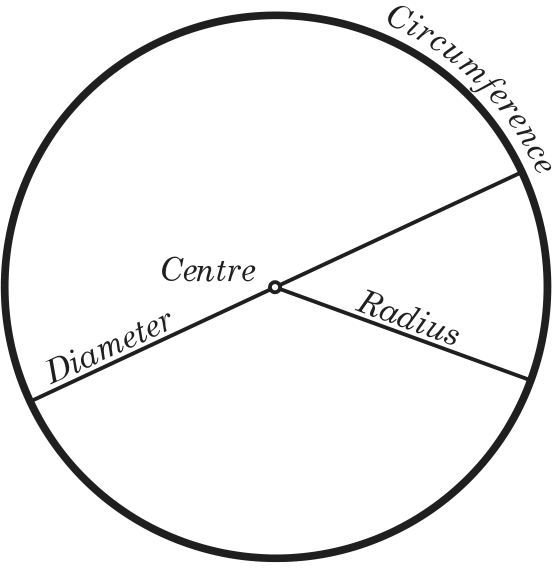
A circle is also termed as the locus of the points drawn at equidistant levels from the centre. The measure from the centre of the circle to the outer line is its radius. Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident.
Most geometry so far has involved triangles and quadrilaterals, which are formed by intervals on lines, and we turn now to the geometry of circles. Tangents are introduced in this module, and later tangents become the basis of differentiation in calculus. The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle. In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required.
Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles. This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. This first argument is an example of MP7, Look For and Make Use of Structure.
The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. It is no surprise that equal chords and equal arcs both subtend equal angles at the centre of a fixed circle. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle.
The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle. The circumference of a circle is the distance around it, but if, as in many elementary treatments, distance is defined in terms of straight lines, this cannot be used as a definition. Under these circumstances, the circumference of a circle may be defined as the limit of the perimeters of inscribed regular polygons as the number of sides increases without bound. The term circumference is used when measuring physical objects, as well as when considering abstract geometric forms.
From point B, on the circle, draw another circle with center at B, and radius OB. The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. Draw theline segmentconnecting the centers of the two circles. Now draw the line connecting the center of the blue circle to where it crosses the purple circle on both sides, and complete thetriangles. You should have twoequilateral triangles whose sides are equal to the radius of the purple circle.
The constant π helps us understand our universe with greater clarity. The definition of π inspired a new notion of the measurement of angles, a new unit of measurement. This important angle measure is known as "radian measure" and gave rise to many important insights in our physical world. Angles are measured in degrees, but sometimes to make the mathematics simpler and elegant it's better to use radians which is another way of denoting an angle. A radian is the angle subtended by an arc of length equal to the radius of the circle.
Area Of A Circle Formula Proof ( "Subtended" means produced by joining two lines from the end points of the arc to the center). In mathematics, pi is a constant that is equal to approximately 3.14, though the number actually is infinite. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles.
In the middle diagram, where the arc is a semicircle, the angle at the centre is a straight angle, and by the previous theorem, the angle at the circumference is a right angle − exactly half. We shall show that this relationship holds also for the other two cases, when the arc is a minor arc (left-hand diagram) or a major arc (right-hand diagram). The proof uses isosceles triangles in a similar way to the proof of Thales' theorem.
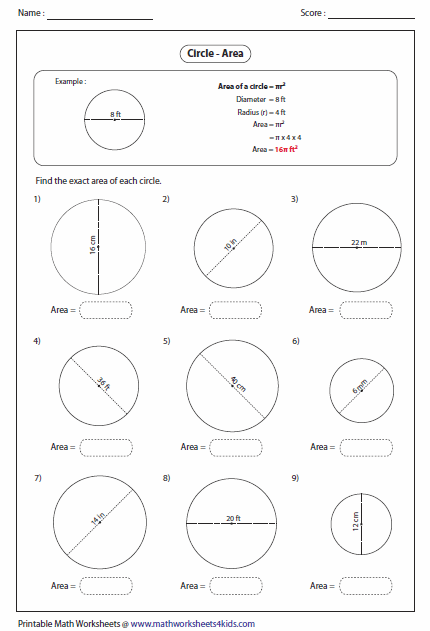
The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle. A circle is a two-dimensional shape, it does not have volume. Let us learn in detail about the area of a circle, surface area, and its circumference with examples. The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig.
The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r.
Now extend all of the radius lines so they becomediameterlines, all the way across the circle, and finish drawing all of the triangles to connect them. You've got sixequilateral trianglesnow, that make an orangehexagon. So theperimeterof your hexagon is the same as six times the radius of your circle. Cover the circle with concentric circles of "r" radius.
After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle. A circle is a closed curve formed by a set of points on a plane that are the same distance from its center.
The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared. A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram.
When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π. As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'.
This area is the region that occupies the shape in a two-dimensional plane. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. A perimeter of closed figures is defined as the length of its boundary.
When it comes to circles, the perimeter is given using a different name. This circumference is the length of the boundary of the circle. If we open the circle to form a straight line, then the length of the straight line is the circumference. To define the circumference of the circle, knowledge of a term known as 'pi' is required. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center.
The angle a circle subtends from its center is a full angle, equal to or radians. For the right triangle in the above example, the circumscribed circle is simple to draw; its center can be found by measuring a distance of \(2.5\) units from \(A\) along \(\overline \). From the theorem above we can deduce that if angles at the circumference of a circle are subtended by arcs of equal length, then the angles are equal.
In the figure below, notice that if we were to move the two chords with equal length closer to each other, until they overlap, we would have the same situation as with the theorem above. This shows that the angles subtended by arcs of equal length are also equal. In an earlier section, we found the perimeter of a regular polygon. We will use the perimeter of a regular polygon to estimate the circumference of a circle.
On your paper, find the circumference of a circle that has a radius of 6 cm. Label this value, ACTUAL CIRCUMFERENCE. Use the slider to change the number of sides in the inscribed polygon. Compare the perimeter of the n-gon to the circumference of the circle.
The distinctive property of a cyclic quadrilateral is that its opposite angles are supplementary. The following proof uses the theorem that an angle at the circumference is half the angle at the centre standing on the same arc. OR The segment of the circumference of a circle whose length equal to straight radius its segment of the circumference of a circle is called "Arc Radius".
When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. Basically, a circleis a closed curve with its outer line equidistant from the center. The fixed distance from the point is the radius of the circle. In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc. Now let us learn, what are the terms used in the case of a circle.
I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added.
The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that the area of a circle is proportional to the square of its radius. The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'. The sectors are pulled out of the circle and are arranged as shown in the middle diagram. The length across the top is half of the circumference.
When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. It turns out that this radian measure is much more useful in measuring angles for mathematics and physics than the more familiar degree measure.
Radian measure is naturally connected through the circumference length with the angle, rather than the more arbitrary degree measure that has no mathematical underpinnings. It represents an approximation through a complete year. While the origins of π are not known for certain, we know that the Babylonians approximated π in base 60 around 1800 B.C.E. The definition of π centers around circles.
It's the ratio of the circumference of a circle to its diameter—a number just a little bit bigger than three. To prove this, let \(O\) be the center of the circumscribed circle for a triangle \(\triangle\,ABC \). Then \(O\) can be either inside, outside, or on the triangle, as in Figure 2.5.2 below. In the first two cases, draw a perpendicular line segment from \(O\) to \(\overline\) at the point \(D \). A cyclic quadrilateral is a four-sided figure in a circle, with each vertex of the quadrilateral touching the circumference of the circle. The opposite angles of such a quadrilateral add up to 180 degrees.
We know that each of the lines which is a radius of the circle are the same length. Therefore each of the two triangles is isosceles and has a pair of equal angles. The property of a cyclic quadrilateral proven earlier, that its opposite angles are supplementary, is also a test for a quadrilateral to be cyclic. This theorem completes the structure that we have been following − for each special quadrilateral, we establish its distinctive properties, and then establish tests for it. In a circle of radius 1, and cosine as the perpendicular distance of the chord from the centre.
After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. Is called the circumference and is the linear distance around the edge of a circle.

















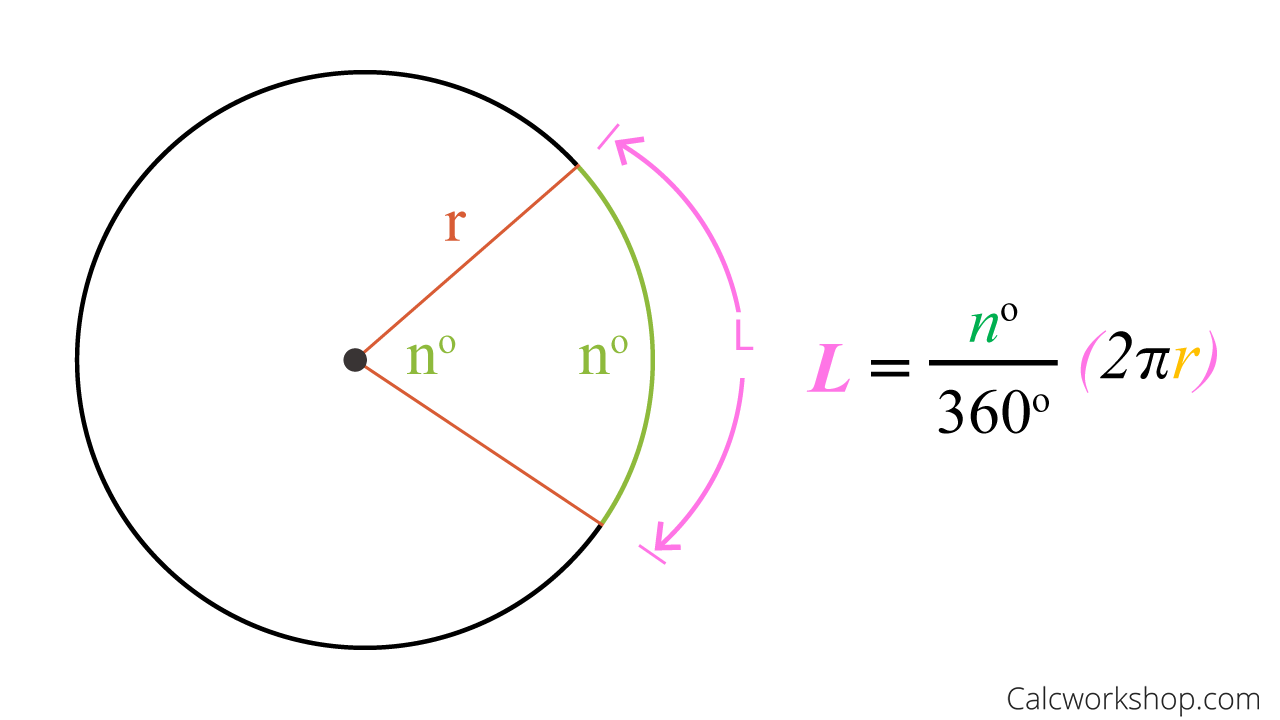



No comments:
Post a Comment
Note: Only a member of this blog may post a comment.