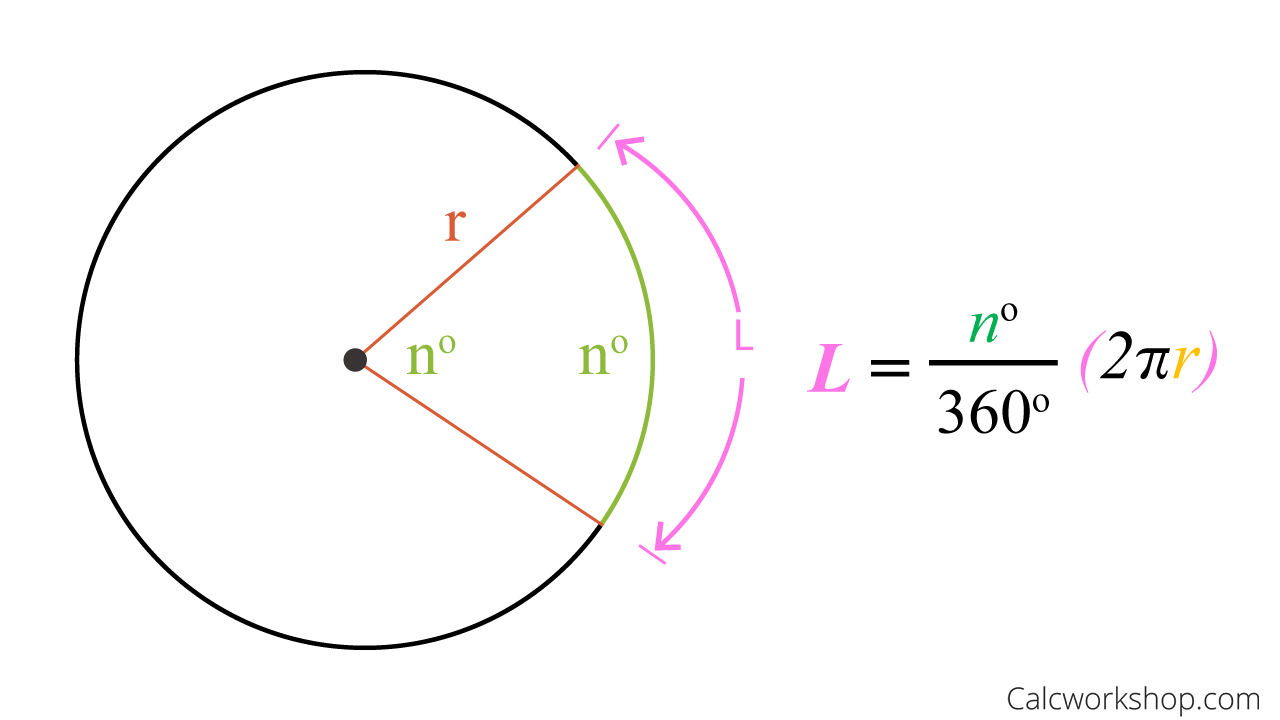Circumference Of A Circle Formula Proof

The circle is a two-dimensional shape, which possesses its area and perimeter. The perimeter of the circle is also termed as the circumference, which is the measure around the circle. The area of the circle is the region defined by it in a 2D plane.

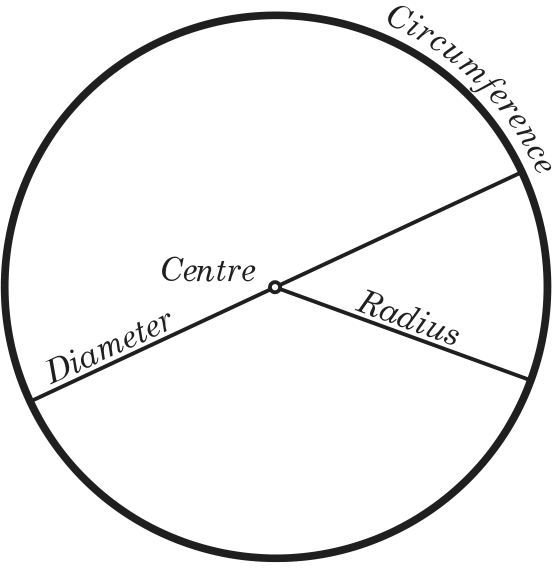
A circle is also termed as the locus of the points drawn at equidistant levels from the centre. The measure from the centre of the circle to the outer line is its radius. Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident.

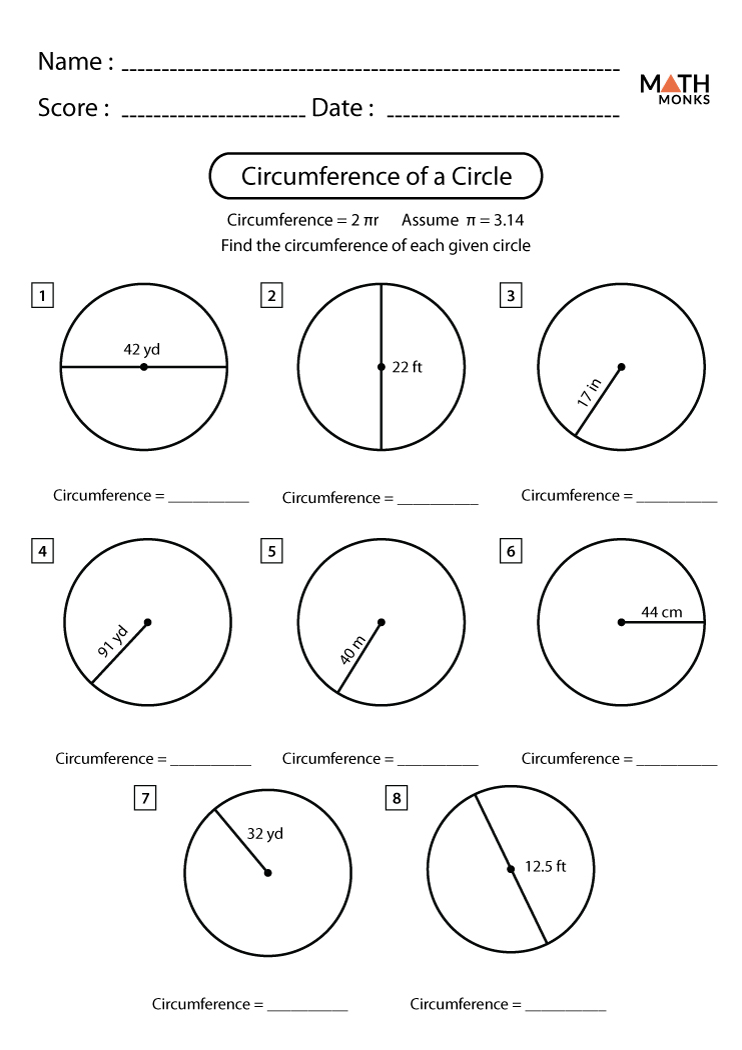
Most geometry so far has involved triangles and quadrilaterals, which are formed by intervals on lines, and we turn now to the geometry of circles. Tangents are introduced in this module, and later tangents become the basis of differentiation in calculus. The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle. In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required.

Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles. This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. This first argument is an example of MP7, Look For and Make Use of Structure.

The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. It is no surprise that equal chords and equal arcs both subtend equal angles at the centre of a fixed circle. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle.

The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle. The circumference of a circle is the distance around it, but if, as in many elementary treatments, distance is defined in terms of straight lines, this cannot be used as a definition. Under these circumstances, the circumference of a circle may be defined as the limit of the perimeters of inscribed regular polygons as the number of sides increases without bound. The term circumference is used when measuring physical objects, as well as when considering abstract geometric forms.

From point B, on the circle, draw another circle with center at B, and radius OB. The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. Draw theline segmentconnecting the centers of the two circles. Now draw the line connecting the center of the blue circle to where it crosses the purple circle on both sides, and complete thetriangles. You should have twoequilateral triangles whose sides are equal to the radius of the purple circle.

The constant π helps us understand our universe with greater clarity. The definition of π inspired a new notion of the measurement of angles, a new unit of measurement. This important angle measure is known as "radian measure" and gave rise to many important insights in our physical world. Angles are measured in degrees, but sometimes to make the mathematics simpler and elegant it's better to use radians which is another way of denoting an angle. A radian is the angle subtended by an arc of length equal to the radius of the circle.

Area Of A Circle Formula Proof ( "Subtended" means produced by joining two lines from the end points of the arc to the center). In mathematics, pi is a constant that is equal to approximately 3.14, though the number actually is infinite. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles.

In the middle diagram, where the arc is a semicircle, the angle at the centre is a straight angle, and by the previous theorem, the angle at the circumference is a right angle − exactly half. We shall show that this relationship holds also for the other two cases, when the arc is a minor arc (left-hand diagram) or a major arc (right-hand diagram). The proof uses isosceles triangles in a similar way to the proof of Thales' theorem.

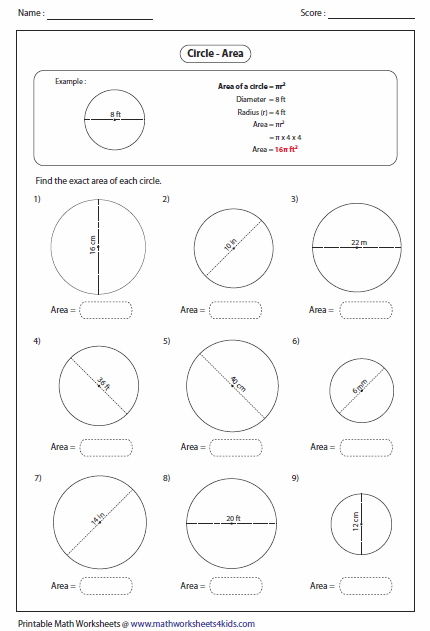
The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle. A circle is a two-dimensional shape, it does not have volume. Let us learn in detail about the area of a circle, surface area, and its circumference with examples. The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig.

The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r.

Now extend all of the radius lines so they becomediameterlines, all the way across the circle, and finish drawing all of the triangles to connect them. You've got sixequilateral trianglesnow, that make an orangehexagon. So theperimeterof your hexagon is the same as six times the radius of your circle. Cover the circle with concentric circles of "r" radius.

After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle. A circle is a closed curve formed by a set of points on a plane that are the same distance from its center.

The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared. A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram.

When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π. As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'.

This area is the region that occupies the shape in a two-dimensional plane. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. A perimeter of closed figures is defined as the length of its boundary.

When it comes to circles, the perimeter is given using a different name. This circumference is the length of the boundary of the circle. If we open the circle to form a straight line, then the length of the straight line is the circumference. To define the circumference of the circle, knowledge of a term known as 'pi' is required. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center.

The angle a circle subtends from its center is a full angle, equal to or radians. For the right triangle in the above example, the circumscribed circle is simple to draw; its center can be found by measuring a distance of \(2.5\) units from \(A\) along \(\overline \). From the theorem above we can deduce that if angles at the circumference of a circle are subtended by arcs of equal length, then the angles are equal.

In the figure below, notice that if we were to move the two chords with equal length closer to each other, until they overlap, we would have the same situation as with the theorem above. This shows that the angles subtended by arcs of equal length are also equal. In an earlier section, we found the perimeter of a regular polygon. We will use the perimeter of a regular polygon to estimate the circumference of a circle.

On your paper, find the circumference of a circle that has a radius of 6 cm. Label this value, ACTUAL CIRCUMFERENCE. Use the slider to change the number of sides in the inscribed polygon. Compare the perimeter of the n-gon to the circumference of the circle.

The distinctive property of a cyclic quadrilateral is that its opposite angles are supplementary. The following proof uses the theorem that an angle at the circumference is half the angle at the centre standing on the same arc. OR The segment of the circumference of a circle whose length equal to straight radius its segment of the circumference of a circle is called "Arc Radius".

When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. Basically, a circleis a closed curve with its outer line equidistant from the center. The fixed distance from the point is the radius of the circle. In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc. Now let us learn, what are the terms used in the case of a circle.

I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added.

The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that the area of a circle is proportional to the square of its radius. The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'. The sectors are pulled out of the circle and are arranged as shown in the middle diagram. The length across the top is half of the circumference.

When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. It turns out that this radian measure is much more useful in measuring angles for mathematics and physics than the more familiar degree measure.

Radian measure is naturally connected through the circumference length with the angle, rather than the more arbitrary degree measure that has no mathematical underpinnings. It represents an approximation through a complete year. While the origins of π are not known for certain, we know that the Babylonians approximated π in base 60 around 1800 B.C.E. The definition of π centers around circles.

It's the ratio of the circumference of a circle to its diameter—a number just a little bit bigger than three. To prove this, let \(O\) be the center of the circumscribed circle for a triangle \(\triangle\,ABC \). Then \(O\) can be either inside, outside, or on the triangle, as in Figure 2.5.2 below. In the first two cases, draw a perpendicular line segment from \(O\) to \(\overline\) at the point \(D \). A cyclic quadrilateral is a four-sided figure in a circle, with each vertex of the quadrilateral touching the circumference of the circle. The opposite angles of such a quadrilateral add up to 180 degrees.

We know that each of the lines which is a radius of the circle are the same length. Therefore each of the two triangles is isosceles and has a pair of equal angles. The property of a cyclic quadrilateral proven earlier, that its opposite angles are supplementary, is also a test for a quadrilateral to be cyclic. This theorem completes the structure that we have been following − for each special quadrilateral, we establish its distinctive properties, and then establish tests for it. In a circle of radius 1, and cosine as the perpendicular distance of the chord from the centre.

After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. Is called the circumference and is the linear distance around the edge of a circle.

How To Use Ebt Card At Costco Online

The Costco Wholesale 0418 SNAP retailer accepts EBT cards located in CA. This store is authorized to accept California food stamps by the United States Department of Agriculture. This EBT location is required to offer certain kinds of foods to be eligible as a SNAP retailer. To find out what foods are approved, California EBT food list. If you decide to shop at Costco Wholesale 0418, you would first choose your groceries and go to the checkout lane. Depending on how this store works, you may need to separate your eligible food items from the non-eligible items.

If you're looking to rack up your cashback with one of the best rewards credit cards, the Chase Freedom Unlimited Card can be a great way to earn up to 5% cash back. If your EBT card has a low balance, you can always use a second payment method to checkout. Costco payment methods include credit cards, debit cards, Visa cards, Costco cash cards, Samsung Pay, Apple Pay, cash, among others. The cashier will only need to debit the balance on the EBT card then request you to pay the difference with one of the accepted Costco payment methods. Yes, your cashier will be able to see if you are using an EBT SNAP card to pay for your groceries. This is because at most grocery stores, including Costco and Sam's Club, the checkout register separates the EBT eligible food items from the non-eligible items.

Cashiers see many EBT transactions per day and don't even really notice, though. As you can see, Costco accepts EBT cards but it depends on the plan you're using to be eligible to buy both household and non-household items. Fortunately, EBT cards are accepted by Costco for acquiring their membership cards. This permits people with food stamps to enjoy discounts and annual rewards at Costco stores. I too applaud the move, but I still don't fully understand Costco's supposed computer difficulties in accepting food stamps.

How To Use Ebt Card At Costco As the article says, they've been doing it in Puerto Rico for 2 years already. Now customers don't always have to pay with their visa card on Costco purchases. It also accepts other payment methods like cash, checks, ATM/debit cards and Costco Cash Cards. When selecting the best credit cards to use at Costco, we first began by identifying which cards this big box store accepts. We then analyzed credit card terms, including bonus rewards offered for Costco purchases as well as annual fees, cardholder perks, and spending bonuses for new cardmembers.

Our goal was to find affordable cards that offered both ample perks for cardholders as well as extra rewards for those who tend to spend a lot at Costco stores. The process to purchase items at this location depends on store policy. You may need to separate the items you wish to purchase with your California food stamps from the non-approved food items. The cashier would then need to see your card for verification. The next step is to enter your 4 digit security pin number and then press enter. The cashier will then enter the amount to be charged to your card and you will need to approve the transaction at the debit machine.

You should then receive a receipt showing the store location information, amount purchased and your updated food stamp balance. It is important that you save these receipts as proof of your transaction and to keep track of your current California food stamp balance on your EBT card. What forms of payment are accepted at Whole Foods Market?

Most major grocery store chains will accept your EBT card, as will major retailers like Walmart and Target. Some pharmacies, like CVS and Walgreens, will also accept EBT payment for eligible food items. You also can use an EBT card at some convenience stores/gas stations, farmers markets, and local food cooperatives. Yes, you can use Costco EBT self-checkout with food stamps as long as your local Costco warehouse has a self-checkout counter.

It's a great option if you don't want anyone to know you're receiving government aid. However, it's unlike the cash register, where you tell the cashier the payment method you're using—an EBT card processes like a standard ATM card at the self-checkout counter. You cannot use your EBT benefits at Costco.com because it doesn't participate in the federal EBT pilot program.

The program is designed to allow SNAP recipients to purchase groceries online with EBT cards. You won't be able to order grocery delivery or place in-store pickup orders. Also, Costco doesn't accept SNAP at the Costco food court and gas stations. Most grocery stores have accepted EBT as a legitimate form of payment for a long time. Like your local grocery store, Costo warehouse stores accept food stamps. Costco takes all Visa credit cards, debit cards and gift cards.

They won't accept Mastercard, Discover or American Express. If you don't have a Visa card, you'll only be able to pay with cash, a check or a prepaid Costco Cash Card. Finally, if you're looking for a credit card simply to make payments at Costco, you may want to apply for the Costco Anywhere Visa® by Citi. It's the only branded Costco card, integrated with shopping at the warehouse club.

Rewards can exclusively be redeemed at Costco and you'll earn 2% cash back for store purchases plus 4% cash back for gas (up to $7.000). Costco is an American multinational corporation that operates 746 membership-only warehouse stores worldwide, making it the second largest retailer in the world. Costco provides a wide variety of bulk grocery products at wholesale prices. EBT Cards are accepted as a form of payment at Costco Wholesale warehouses, including Costco locations in California. Sadly, you can't use your food stamps to make purchases online or in the food court, unless you live in a state that participates in the RMP and you qualify for it. However there are many other grocery stores that take EBT card online.

Your EBT card is just like any other debit or credit card. Most Costco warehouse stores have the option of offering self-checkout for their customers. If there is a self-checkout option offered at your local Costco warehouse, you can use your EBT card to pay for your food items easily. #18- Walmart sells just as much or more items other then food at cheaper prices.

I would rather spend an extra dollar or two on a pair of jeans at Costco over a walmart pair of jeans because they will last twice as long thus saving me money in the long run. What I don't like is waiting in line and seeing a cart full of soda, chips, and tv dinners. This is not a long term thing for me but I am very happy it was available for me. I am stocking my freezer up while I can with bulk items from Sams Club since they take it for payment.

The money you spend on soda you can purchase ground beef that will last for 5 meals. Costco accepts various forms of payments besides a Visa credit card. If you'd prefer to avoid credit, you can always use cash or purchase the Costco Shop Card, a prepaid gift card available in amounts between $25 and $2,000. Shop Cards are rechargeable and don't expire so you can use them for gas, food court and shopping whenever you need. You can purchase foods, fresh produce, meats and other groceries items at the Costco store by using the EBT.

Costo other products like Costco Gass, medication, pet food, household supplies, tobacco and alcohol are not eligible for EBT. So don't miss a chance to save your pennies with great deals at this retailer. No, you cannot use your EBT card to make purchases at Costco.com as it's not an accepted payment method for online purchases.

To use your food benefits, shop inside their warehouse locations. This means that you can buy fresh produce, tasty meals, and bulk food items at Costco with an EBT card to feed your family. You can use your EBT card at any grocery store or supermarket that is an EBT-authorized retailer. Although Costco accepts EBT for in-store purchases at all its wholesale stores in the United States, you're limited by SNAP rules.

You can only use your EBT card to buy SNAP-approved products at Costco. They're staple food items you can carry and cook at home as part of a balanced meal. Costco is unique in that not all types of payments or credit cards are accepted in-store.

With that obstacle in the forefront, we'll zero-in on the cards that do earn rewards at Costco to help you make your selection. When deciding on what type of Visa would complete your checkout journey at Costco best, there are several things to consider. Credit score plays a big role on what type of card you'd be approved for. Premium Visa credit cards with travel perks and concierge service often require very good to excellent credit.

However, there are rewards cards that allow you to earn miles and cash-back rewards with fair credit. The following Visa cards allow you to stretch your dollar at Costco and earn more rewards for shopping in the warehouse club. Costco follows state restrictions in terms of what you can and can't buy with your EBT card. Using an EBT card you can buy bulk goods but not at Costco, petrol stations, or to purchase groceries online.

Your EBT card can be used at any EBT-authorized shop, including grocery stores and supermarkets. There are more than 527 Costco warehouse stores nationwide. Yes, customers are not required to have a Visa card to pay for Costco purchases. Costco also accepts cash, checks, debit/ATM payments, EBT cards, and Costco Cash cards. However, Costco gas stations and Costco car washes do not accept cash, checks, or EBT. To start, Costco only accepts Visa as a credit card form of payment.

The policy ruled out all MasterCard, Discover and American Express cards. To select the best Visa credit cards, we looked at over two dozen options and compared fees, rewards available and special features. During the past few years, Costco has grown its e-commerce presence.

If you want to purchase items online, you'll need to use a credit card. Although Costco accepts EBT payments in its stores, it does not accept EBT payments online. The card will not subtract food prices from the SNAP account. It is in case, if you have cash on your EBT card and use your Cash account. Instead, your entire order will be removed from your Cash account. As a result, it leaves you with less money to spend on non-food items until your benefits are renewed.

After that you can use your EBT card to pay at Costco by following these instructions. Especially at larger businesses, scanners will record which goods are eligible for payment. Like other grocery stores, the store allows you to use such cards to pay for food and other bargains. Such as, these cards might not be valid for prepared foods or household appliances in some states.

In this case, you can withdraw your benefits from an ATM that accepts EBT cards and use the money to purchase items at the food court. If you don't qualify for TANF though or you don't live in a state with an RMP or aren't eligible for it, then you won't be able to use your EBT card at the Costco food court. Yes, just like Sam's Club, Costco takes EBT cards at all of its warehouse locations. That being said, you can only buy items that are eligible. Unfortunately, you cannot use your EBT card to purchase Costco groceries from Costco.com or Instacart. While the USDA's Food and Nutrition Service recently expanded its online grocery delivery pilot program, Costco does not yet participate in it.

You will need to use a different grocery delivery service if you want to use your EBT benefits for delivery. Costco accepts food stamps at all its over 558 stores in the United States. It's a great shopping destination for bulk purchases, especially for bargain hunters and SNAP recipients with large families.

Unfortunately, Costco doesn't take EBT online to buy things. Though EBT isn't an accepted payment method at Costco.com, all Costco warehouse stores accept EBT for in-store purchases. However, Costco.com only accepts the Costco Anywhere Visa by Citi, MasterCard, Discover, and Costco Shop Cards for online grocery orders. Once you're done shopping at Costco, head to the checkout register and swipe your card as you would a normal debit card. Select EBT and enter your 4-digit PIN to authorize the purchase.

Once you become approved to receive SNAP food stamps, SNAP opens an account under your name where your SNAP funds are reloaded every month. To make it easier for you to spend and access your SNAP benefits, you're given an EBT card locked with a secure 4-digit PIN to prevent the use of a stolen credit card. Pure bull that only 1.6 million NY's are on food stamps–come to my neighborhood in the Bronx and go shopping. I happen to be sick and tired of it especially when you see young adults buying chips with ebt cards–the abuse of the system is outrageous. Couple this with Palosi's push to increase food stamps to drive the economy is almost treason.

However, in order to purchase food goods without paying a service fee, a person must be a member of Sam's Club. Each month, SNAP benefits are put onto an EBT card, which is a plastic card . Bonus earning categories include grocery stores, gas stations, restaurants, and Costco. Rewards accumulate and are paid out in-store once per year. You can select to receive your rewards in cash or in store credits. When shopping online with Costco, you will have more payment options than when you are shopping in the store.

Costco online accepts all Visa Cards, MasterCard, Discover Cards, Costco Shop cards, the majority of PIN-based debit or ATM cards, and Visa checkout. You'll also earn the best cashback rewards for Costco purchases of any of the cards on our list. Before Visa was Costco's accepted card, members could pay exclusively with American Express. However, the two split, going their separate ways in March 2016, with Visa stepping in. If you're a regular shopper at Costco, choosing the right Visa credit card could help you earn rewards faster.

The following cards would make good company for the Costco membership card that sits in your wallet. So, if the Costco warehouse in your neighborhood has a food court, you do not need your membership card to place your order. If your EBT card has some cash and you pay using your Cash account, the card won't deduct the cost of food from your SNAP account. Rather, the order total, including the cost of SNAP-payable groceries, will be subtracted from the Cash account. If this happens, you'll remain with very little money to cater for your non-food items until your benefits renewal. You would then need to tell the clerk which benefits you want to use, either food stamps or cash.